位错密度和迁移率对淬火中碳马氏体钢低温回火屈服行为的影响
Impact of Dislocation Density and Mobility on Yielding Behavior in Quenched Medium-carbon Martensitic Steel Tempered at Low Temperature
位错密度和迁移率对淬火中碳马氏体钢低温回火屈服行为的影响
中碳马氏体钢是机械零件的重要材料,其力学性能引起了人们的广泛关注。然而,淬火后材料弹性极限的下降是一个遗留的谜题。本文通过中子衍射线剖面分析定量表征了淬火状态和回火状态马氏体钢中的位错密度及其结构,并讨论了它们对屈服应力的影响。淬火态的位错密度最高,为9.7 × 1015 m−2,随回火温度的升高而降低。此外,随着回火温度的升高,刃型位错和螺旋位错的构成比例分别减小和增大。在220℃~ 290℃回火温度下,位错排列参数(M)发生变化。虽然由拉伸试验得到的屈服应力与由位错密度估计的屈服应力存在较大差异,但用M值的倒数作为显示位错有效密度比的指标可以对实验结果进行修正。关键词:马氏体;中碳钢;中子衍射;谱线轮廓分析;移动位错;弹性极限;屈服应力
1. 引言
钢是制造机械产品最常见的工程材料。它具有生产效率高、材料强度高等优点,可通过选择钢种、添加元素或热处理工艺进行控制所需要的性能。[1~3]特别是中高碳钢的淬火可使其淬硬,因此很容易提高其硬度和极限抗拉强度(抗拉强度)。因此,中、高碳钢是工业上轴承和齿轮的重要材料。由于淬火时的材料是脆性的,韧性较低,淬火后需要进行回火,以抑制脆性,提高韧性。Muir等人报道了钢中含碳量(0.2、0.41和0.82 wt%C)的弹性极限、屈服强度和抗拉强度的变化与回火温度有关。[1]随后,对马氏体与热处理及其与力学性能的对应关系进行了许多研究。[3~7]淬火马氏体通常含有大量位错,表现出较高的抗拉强度。虽然淬火材料的弹性极限低得惊人,但它可以通过回火来提高。[1,7]对淬火马氏体弹性极限显著低的原因有一个普遍的认识,可以为淬火碳钢开发更优的热处理条件。Galindo等人证明了板条马氏体屈服应力的综合预测。[8]虽然其模型可以预测屈服应力,但不能计算出淬火或低温回火马氏体弹性极限的降低。淬火材料弹性极限降低的几个原因已经被提出,如移动位错、[9,10]残余奥氏体、[11]和晶间应力;[11,12] 然而,这些还没有被完全证实。对位错结构等微观结构的研究通常使用透射电镜进行。然而,x射线和中子衍射被认为是有前途的替代检验技术。衍射线轮廓的形状取决于试样金属的结晶度;因此,线的轮廓增宽是由于金属晶粒内存在大量晶格缺陷所致。[13]利用物理模型对实测的衍射线形貌进行反分析,就有可能对位错等晶格缺陷进行广泛的研究。[10,14~20]特别是由于马氏体具有较高的位错密度,衍射线形貌分析(LPA)具有很大的优势。此外,由于该测量体积为立方毫米尺度,因此在统计精度方面具有优势,有望与宏观力学特性具有较高的相关性。因此,一些研究尝试使用中子衍射来表征板条马氏体中的位错密度和亚结构。[19,21,22]除了被广泛报道的物理量,如分析中的位错密度和晶粒尺寸,还可以获得位错排列和特征的其他指标。[23~26]因此,在淬火和回火中碳钢的LPA中,我们重点研究了位错密度和前面提到的预计会提示位错结构的参数。讨论了LPA测定的显微组织特征对屈服应力的影响。
2. 实验
2.1. 试样
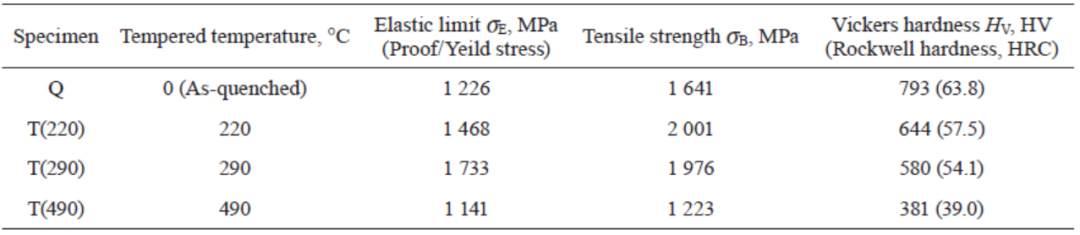
使用的是含0.56%C的中碳钢(相当于AISI 1552标准的钢种)。将该材料加热到830°C,并保持3小时,它们在冷的淬火油中淬火。淬火后,每个试样被加热到若干温度(140℃、290℃和490℃) 1小时,然后在空气中冷却。光学显微镜图像如图1所示。[7]表面经过镜面抛光后,用硝酸溶液蚀刻。从拉伸试验中得到的应力-应变曲线如图2所示,这在以前的研究中已经报道过了。[7]本研究仅采用内部断裂点的结果,拉伸和硬度试验的力学性能见表1。以0.2%的弹性应力为屈服应力和弹性极限,本研究记为屈服应力。

图1 淬火(Q)和回火试样的显微光学图像。淬火之后回火分别在220℃、290℃和490℃ (对应图中T(220)、T(290)和T(490))温度下进行
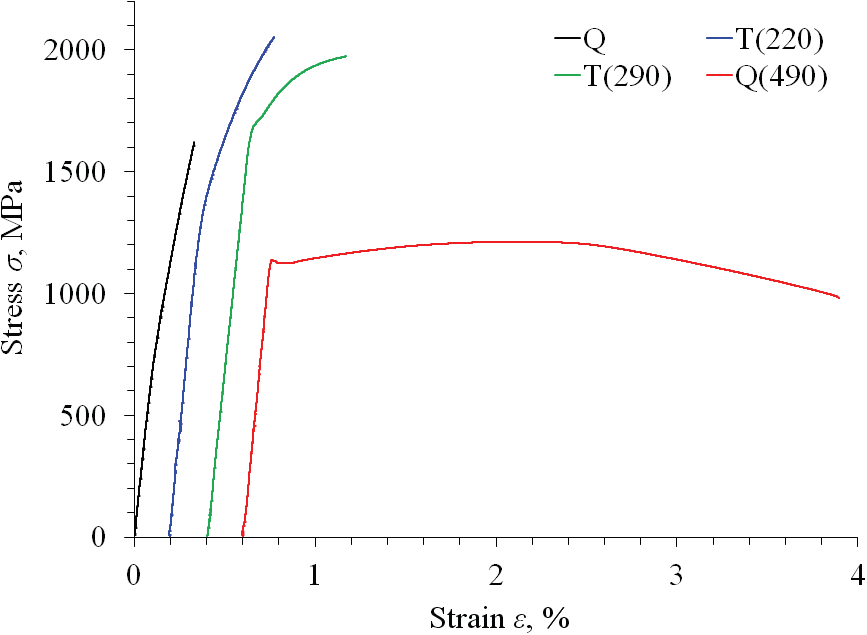
图2 淬火(Q)和回火试样的应力-应变曲线。淬火后在220℃、290℃、490℃温度下回火(分别图中对应T(220)、T(290)、T(490))。[7]应变分别表示为沿水平轴的偏移量表1 淬火(Q)和回火试样的力学性能。淬火后在220℃、290℃、490℃温度下回火(分别图中对应T(220)、T(290)、T(490))。[7]
2.2. 中子衍射测量与分析
中子实验用圆柱形试样直径φ5.5 mm,长度10 mm。高位错密度材料的衍射线轮廓相对较宽较低,此外,残余奥氏体的衍射线与马氏体的衍射线重叠。因此,实验应使用毫米尺度测量体积和高束流通量的中子束进行。因此,在日本质子线加速器的BL20(iMATERIA)上进行了中子衍射测量),[27]积累时间为15分钟,质子加速器功率为500 kW。由于获得的剖面形状分辨率较高,因此仅使用背反射阵列探测器进行测量。为了定量获得位错密度及相关特征,利用卷积多重整体轮廓(CMWP)拟合软件进行LPA。[28,29]在软件中,物理参数被细化到计算的线轮廓,使其接近于测量的线轮廓。物理参数为:q =位错特征,m =晶粒尺寸分布中位数,σ =晶粒尺寸分布的分布,ρ =位错密度,m =位错排列参数,其中晶粒尺寸D为D = m exp(2.5σ 2)。[30,31]散射矢量K≈6-13.5 nm−1之间的线廓线用于分析。晶格常数为0.2866 nm,[32] <111>{110}的Burgers矢量长度为0.2482 nm。通过ANIZIC[33]计算得到h00反射的平均对比度系数为0.284,其弹性刚度分别为c11 = 228、c12 = 132和c44 = 116.5GPa。[34] 利用六硼化镧粉末的衍射线轮廓确定了仪器展宽系数。
3. 结果
图3显示了每个试样的衍射线分布图。在淬火态和回火温度低于290℃的试样中均观察到马氏体和奥氏体的衍射峰。
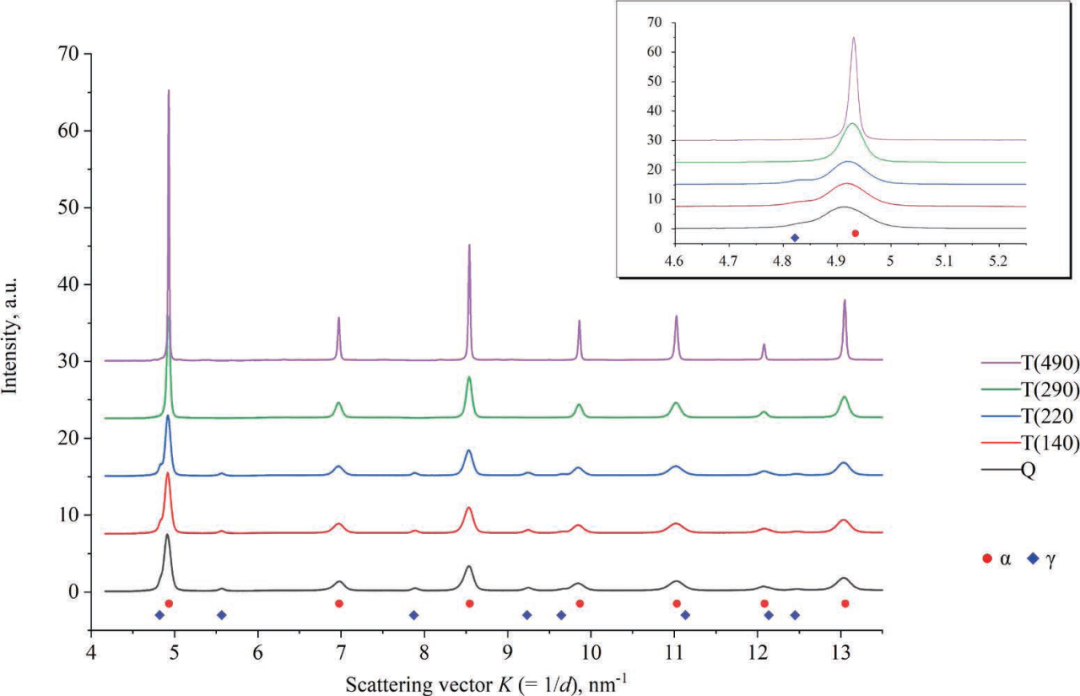
图3 中子衍射线剖面。每个线条的强度为可见性任意偏移。马氏体(α)的衍射峰在所有线条中都能很好地识别。右上角窗口是K = 5 nm−1附近的放大图。奥氏体(γ)的衍射在淬火试样上被识别,而峰强度在回火后下降。最终,在290°C的回火温度下,峰值消失图4为线廓拟合得到的参数:位错密度(ρ)、位错特征(q)、排列参数(M)和晶粒尺寸(D)。淬火试样的位错密度为ρ ~ 1 × 1016 m−2,随回火温度的升高而降低。490℃回火后的试样位错密度为7 × 1014 m−2。螺旋位错和刃型错的q值在淬火后为1.82,随着回火温度的升高,q值增加到2.26;ANIZIC[33]计算出纯的刃型位错和纯的螺旋位错的q值分别为1.29和2.64。这意味着在淬火后的试样中,刃型位错的比例大致是平均的,而回火后螺旋位错的比例是增加的。类似的结果也被Shi等人报道过。[21]在高温下,刃型位错会因攀移而优先湮灭。因此,螺旋位错与刃型位错的比例增加。在淬态试样中,表示位错排列的M值较大,为M≈5。这意味着位错在淬火试样中是随机存在的。在220℃回火时,该值没有降低,而在290℃回火时,该值急剧下降。我们认为在该温度范围内(220-290°C)位错发生了明显的移动,并且相互干扰。
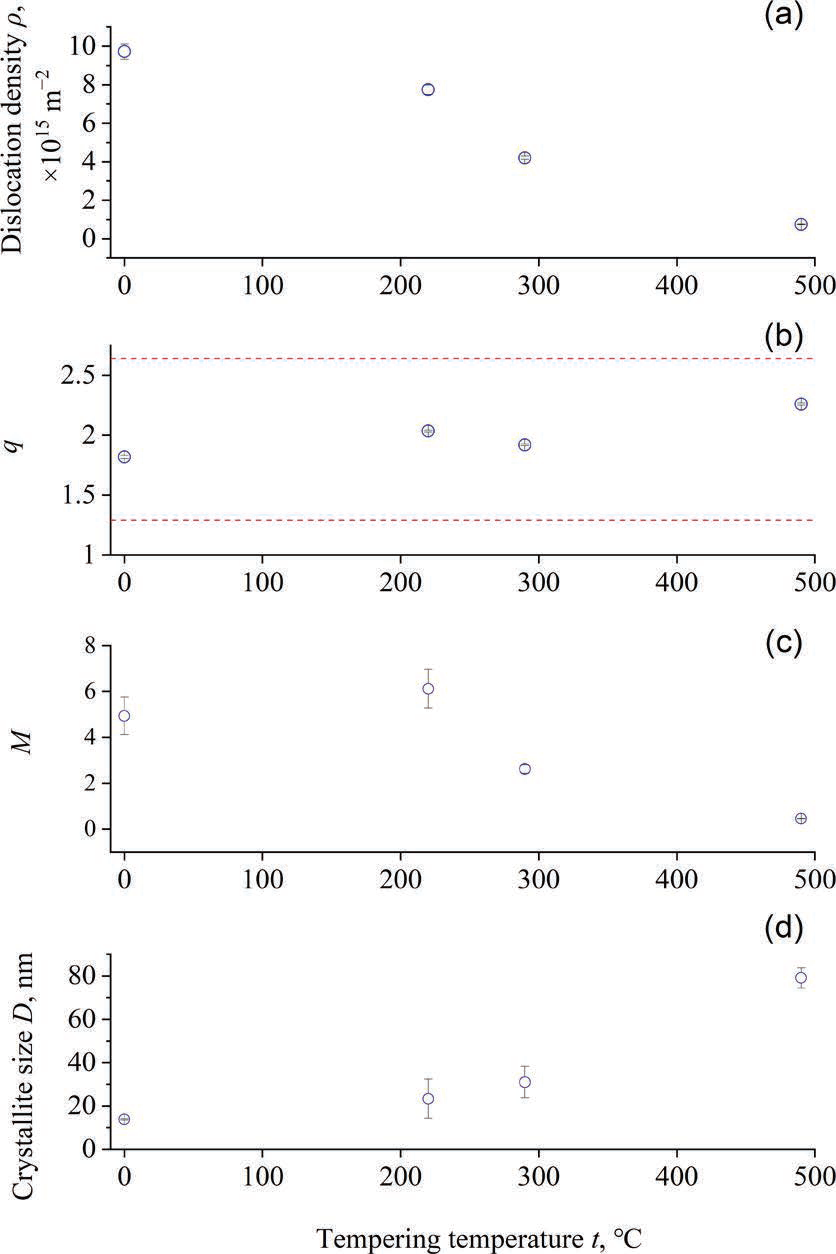
图4 通过LPA从上到下得到了与回火温度有关的参数:位错密度(ρ)、位错特征(q)、排列参数(M)和晶粒尺寸(D)。0°C温度表示未回火的淬火状态
4. 讨论
虽然位错密度随回火温度的升高而降低(图4(a)),但屈服应力在290℃以下增加(图2和表1)。由于常规定律[9,35~37]所制定的加工硬化,屈服应力会降低。在超低碳马氏体钢中,0.2%的弹性应力与位错密度的两个关系为σ0.2=100+1.2×10−5ρ1/2 [MPa]。[9] 利用该公式,假设屈服应力与位错密度的平方根之间的斜率没有改变,即使碳含量变化,也仅仅是截距上的不同,这样可以估计出屈服应力。在这里,我们确定近似线的截距(885 MPa)为近似线与屈服应力实验结果之间的残差平方和最小,由此,得到如下方程:
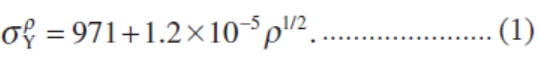
图5显示了使用公式(1)和实验结果(表1)估计的每个试样的屈服应力。淬火试样和220°C回火试样的估计应力明显大于拉伸试验得到的实验结果。
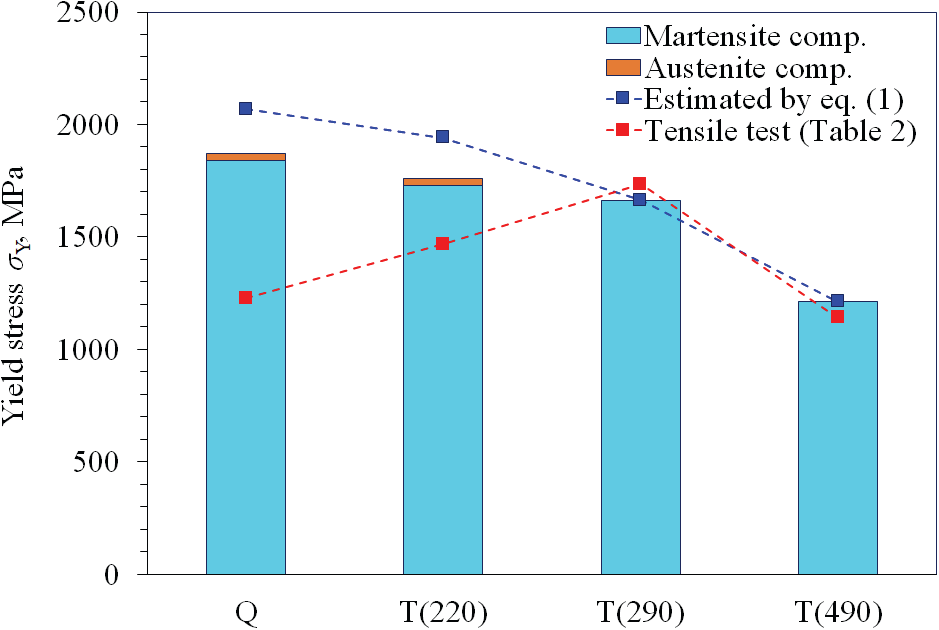
图5 利用公式(1)由位错密度估计屈服应力,并通过拉伸试验测量屈服应力(蓝色和红色图)。条形说明屈服应力在马氏体和残余奥氏体相上的分配为了考虑残余奥氏体的影响,使用软件(MAUD[38])测定了每个试样中的奥氏体相体积分数。在分析中,使用了7个阵列探测器(31、39、81、90、99、162和149),[27]得到的所有中子衍射线剖面。在淬火状态和220°C回火的试样中,每个试样的体积分数为11%,在290°C和490°C回火的试样中无法识别。在290℃以下回火条件下,残余奥氏体的析出发生变化。因此,作为屈服应力需考虑残余奥氏体的影响。当各相屈服应力为σYα和σYγ时,屈服应力可表示为马氏体和奥氏体组分的和,其中残余奥氏体组分为Rγ。图6还给出了马氏体σYα(1−Rγ)和奥氏体σYγRγ的屈服应力估计分量。采用固溶加热的SUS316奥氏体不锈钢,291 MPa的0.2%弹性应力作为奥氏体屈服应力。[16]这个值并不代表当前试样中残余奥氏体的确切屈服应力,而是固溶加热不锈钢中奥氏体的值,它可能小于真实值(奥氏体的分配被高估了)。残余奥氏体对真实屈服应力的影响估计要小于这一结果,由于马氏体相的减少,从公式(1)得到总体屈服应力的值下降,并接近拉伸试验得到的数值。然而,修正并不足以解释实验和估计屈服应力之间的差距。虽然存在残余奥氏体的影响,但这意味着还有其他主要因素。由于渗碳体的体积分数明显小于残余奥氏体的体积分数,因此它不是降低屈服应力的主要因素。
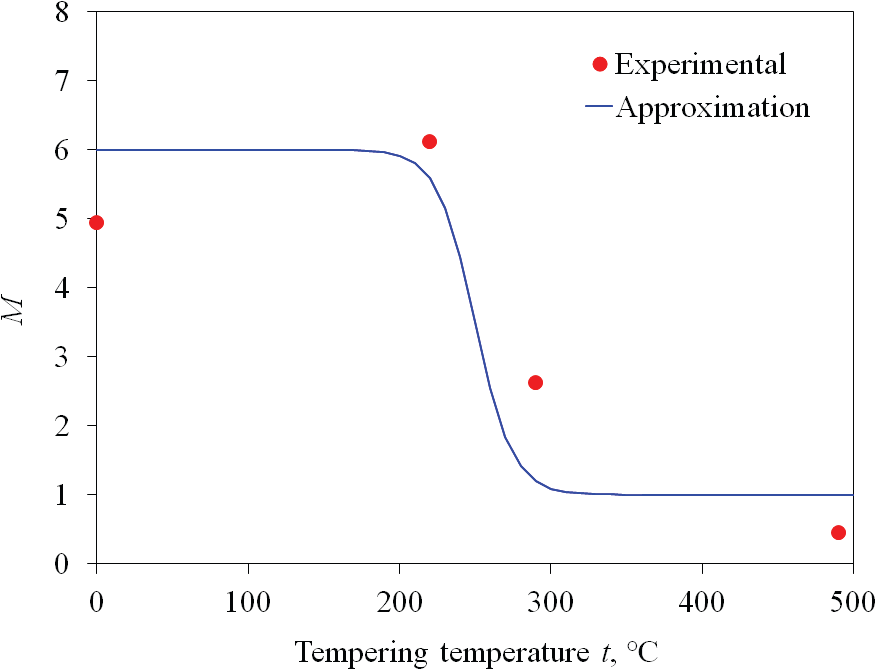
图6 M值作为由公式(2)确定的温度的函数。M值在220°C到290°C之间急剧变化如前所述,残余奥氏体并不是导致屈服应力下降的主要原因。然而,移动错位可能是一个原因。Takaki等人解释说,由于超低碳马氏体钢中可移动位错的增加,流动应力与位错密度的平方根不成正比。[9]位错独立排列时,排列参数M较大,当位错相互干扰形成偶极子排列时,M变小。[23,28]另一方面,独立存在的位错移动相对来说容易,位错相互纠缠或形成偶极子,使其难以移动。假设独立存在且相对容易移动的位错为移动位错,则参数M代表可动位错数量的定量趋势,对屈服应力没有影响。因此,我们的目标是通过使用M值从总位错密度中消除移动位错分量来表达对屈服应力有贡献的位错密度,即有效位错密度。由于M值对线廓形很敏感,分析结果有较大的散射,M值用以下方程作为回火温度(T)的函数来近似表达:
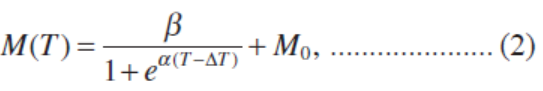
其中参数α、β、M0和ΔT为常数。请注意,函数及其变量的选择是任意的,以重现实验结果。图6显示了由公式(2)近似的M值的直线。α = 0.08℃−1,β = 5, M0 = 1, ΔT = 250°C。为得到有效位错密度ρeff,将总位错密度(ρ)与有效系数相乘,得到的M (T)的倒数用M0归一化,如下:
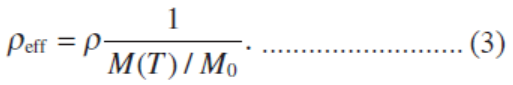
根据各试件的有效位错密度,采用公式(1)计算屈服应力,如图7所示。由于加工硬化,与总位错密度相关的原始图向近似线附近移动,由此可知,由M值估计的有效位错密度为加工硬化分量。根据位错的有效密度,将屈服应力与位错密度的关系近似为σY eff= 667 + 1.77 ×10−5ρeff 1/2。
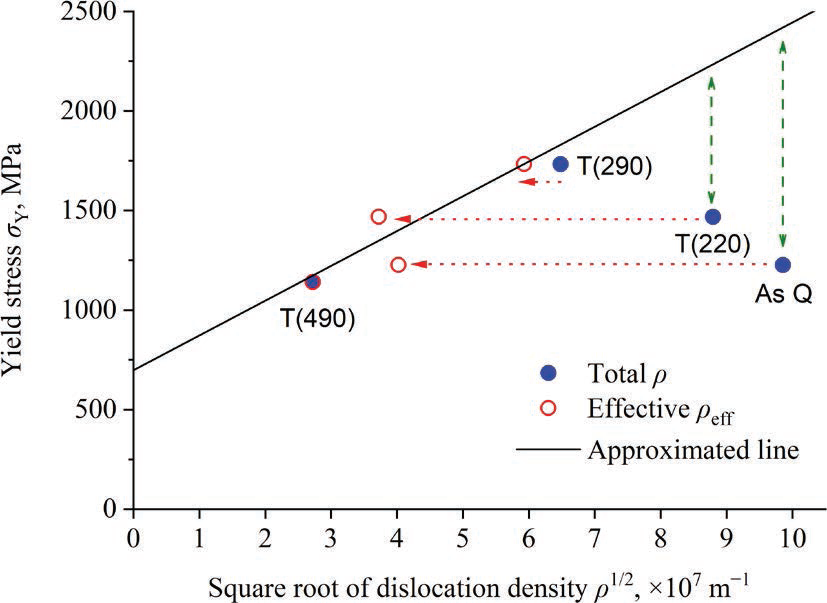
图7 屈服应力对位错密度平方根的影响,并用M值作为有效位错密度的修正。有效位错密度接近于位错硬化的近似线
5. 结论
采用中子LPA法研究了调质态中碳钢的位错密度和组织对拉伸屈服行为的影响。淬态试样的总位错密度最高,随回火温度的升高而降低。然而,屈服应力与位错总密度无关。在本研究中,低温回火(< 290°C)后,由总位错密度估算的屈服应力显著高于拉伸试验测量的屈服应力。残余奥氏体对屈服应力的降低有一定的贡献,但不是主要的影响因素。用位错排列参数作为可动位错的组分比来确定位错的有效密度和屈服应力,可以很好地解释实验结果。
致谢
J-PARC材料与生命科学实验设施的中子实验是在一个项目(计划号2019AM0026)下进行的。
参考文献
1) H. Muir, B. L. Averbach and M. Cohen: Trans. Am. Soc. Met., 47 (1955), 380.2) H. Bhadeshia and R. Honeycombe: Steels: Microstructure and Properties, 3rd ed., Butterworth-Heinemann, Oxford, UK, (2006), 1.3) G. Krauss: Steel Res. Int., 88 (2017), 1700038. https://doi.org/10.1002/ srin.2017000384) G. R. Speich and W. C. Leslie: Metall. Trans., 3 (1972), 1043. https://doi.org/10.1007/BF026424365) R. A. Grange, C. R. Hribal and L. F. Porter: Metall. Trans. A, 8 (1977), 1775. http: // link. springer. com/ article/ 10. 1007/ BF026468826) D. C. Saha, E. Biro, A. P. Gerlich and Y. Zhou: Mater. Sci. Eng. A, 673 (2016), 467. https: // doi. org/ 10. 1016/ j.msea. 2016.07.0927) J. Shimbe, M. Kumagai, A. Tanabe and Y. Mizuno: Trans. Jpn. Soc. Mech. Eng., 87 (2021), 21-00082. https: // doi. org/ 10.1299/transjsme.21-000828) E. I. Galindo-Nava and P. E. J. Rivera-Díaz-del-Castillo: Acta Mater., 98 (2015), 81. https: // doi. org/ 10. 1016/ j. actamat. 2015.07.0189) S. Takaki, K.-L. Ngo-Huynh, N. Nakada and T. Tsuchiyama: ISIJ Int., 52 (2012), 710. https: // doi. org/ 10. 2355/ isijinternational.52.71010) D. Akama, T. Tsuchiyama and S. Takaki: ISIJ Int., 56 (2016), 1675. https: // doi. org/ 10. 2355/ isijinternational.ISIJINT-2016-14011) M. A. Zaccone and G. Krauss: Metall. Trans. A, 20 (1989), 188. https://doi.org/10.1007/BF0264750712) B. Hutchinson, D. Lindell and M. Barnett: ISIJ Int., 55 (2015), 1114. https: // doi. org/ 10. 2355/ isijinternational.55.111413) B. E. Warren: X-Ray Diffraction, Dover Publications, New York, (1990), 264.14) G. K. Williamson and W. H. Hall: Acta Metall., 1 (1953), 22. https://doi.org/10.1016/0001-6160(53)90006-615) T. Ungár and A. Borbély: Appl. Phys. Lett., 69 (1996), 3173. https://doi.org/10.1063/1.11795116) M. Kumagai, K. Akita, M. Imafuku and S. Ohya: Adv. Mater. Res., 996 (2014), 39. https: // doi. org/ 10. 4028/ www. scientific.net/AMR.996.3917) W. Gong, Y. Tomota, S. Harjo, Y. H. Su and K. Aizawa: Acta Mater., 85 (2015), 243. https: // doi. org/ 10. 1016/ j. actamat.2014.11.02918) T. Ungár, S. Harjo, T. Kawasaki, Y. Tomota, G. Ribárik and Z. Shi: Metall. Mater. Trans. A, 48 (2017), 159. https: // doi. org/10.1007/s11661-016-3845-419) S. Harjo, T. Kawasaki and S. Morooka: Adv. Exp. Mech., 2 (2017), 112. https://doi.org/10.11395/aem.2.0_11220) M. Kumagai, M. E. Curd, H. Soyama, T. Ungár, G. Ribárik and P. J. Withers: Mater. Sci. Eng. A, 813 (2021), 141037. https://doi.org/10.1016/j.msea.2021.14103721) Z. M. Shi, W. Gong, Y. Tomota, S. Harjo, J. Li, B. Chi and J. Pu: Mater. Charact., 107 (2015), 29. https: // doi. org/ 10. 1016/j.matchar. 2015.06.04022) Y. Wang, Y. Tomota, T. Ohmura, S. Morooka, W. Gong and S. Harjo: Acta Mater., 184 (2020), 30. https: // doi. org/ 10. 1016/j.actamat.2019.11.05123) M. Wilkens: Phys. Status Solidi A, 2 (1970), 359. https://doi.org/10.1002/pssa.1970002022424) T. Ungár, J. Gubicza, G. Ribárik and A. Borbély: J. Appl. Crystallogr., 34 (2001), 298. https: //doi. org/ 10. 1107/ S002188980100371525) M. Moshtaghi and S. Sato: ISIJ Int., 59 (2019), 1591. https://doi.org/10.2355/isijinternational.isijint-2019-07726) M. Kumagai, K. Akita, M. Kuroda and S. Harjo: Mater. Sci. Eng. A, 820 (2021), 141582. https: // doi. org/ 10. 1016/ j. msea.2021.14158227) Y. Onuki, A. Hoshikawa, S. Sato, P. Xu, T. Ishigaki, Y. Saito, H. Todoroki and M. Hayashi: J. Appl. Crystallogr., 49 (2016), 1579. https://doi.org/10.1107/S160057671601164X28) G. Ribárik: Ph.D. thesis, Eötvös Loránd University, (2008).29) G. Ribárik, B. Jóni and T. Ungár: J. Mater. Sci. Technol., 35 (2019), 1508. https: // doi. org/ 10. 1016/ j. jmst.2019.01.01430) J. I. Langford, D. Louër and P. Scardi: J. Appl. Crystallogr., 33 (2000), 964. https://doi.org/10.1107/S002188980000460X31) G. Ribárik, T. Ungár and J. Gubicza: J. Appl. Crystallogr., 34 (2001), 669. https: // doi. org/ 10. 1107/ S002188980101145132) W. B. Pearson: A Handbook of Lattice Spacings and Structures of Metals and Alloys, Vol. 2, Pergamon Press, Oxford, UK, (1967), 82.33) A. Borbély, J. Dragomir-Cernatescu, G. Ribárik and T. Ungár: J. Appl. Crystallogr., 36 (2003), 160. https: //doi.org/10.1107/S002188980202158134) A. E. Lord, Jr. and D. N. Beshers: J. Appl. Phys., 36 (1965), 1620. https://doi.org/10.1063/1.170309835) J. E. Bailey and P. B. Hirsch: Philos. Mag., 5 (1960), 485. https://doi.org/10.1080/1478643600823830036) M. Kumagai, M. Imafuku and S. Ohya: ISIJ Int., 54 (2014), 206. https: //doi. org/ 10. 2355/ isijinternational. 54. 20637) M. Kumagai, M. Kuroda, K. Akita, M. Kamaya and S. Ohya: Mater. Sci. Forum, 941 (2018), 376. https: // doi.org/10.4028/www.scientific. net/MSF.941.37638) L. Lutterotti, S. Matthies, H.-R. Wenk, A. S. Schultz and J. W. Richardson, Jr.: J. Appl. Phys., 81 (1997), 594. https: // doi.org/10.1063/1.364220
作者
Hiroyuki UCHIMA,1) Masayoshi KUMAGAI,2)* Junzo SHIMBE,1) Akihiro TANABE,1) Yuta MIZUNO1) and Yusuke ONUKI3):1) THK Co., Ltd, 2-12-10 Shibaura, Minato-ku, Tokyo, 108-8506 Japan.2) Department of Mechanical Systems Engineering, Faculty of Science and Engineering, Tokyo City University, 1-28-1 Tamazutsumi, Setagaya-ku, Tokyo, 158-8557 Japan.3) Frontier Research Center for Applied Atomic Sciences, Ibaraki University, 162-1 Shirakata, Tokai, Ibaraki, 319-1106 Japan.通讯作者E-mail: mkumagai@tcu.ac.jp
唐杰民2022年6月下旬在安徽黄山市屯溪翻译自某国<ISIJ International>今年5月期刊,水平有限,有不对不妥之处请各位看官给与指正。





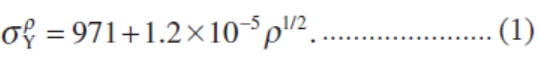


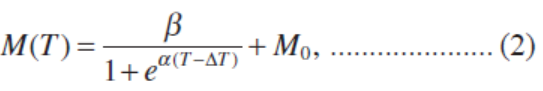
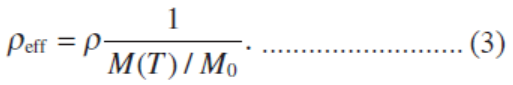








 欢迎你第一次访问网站!
欢迎你第一次访问网站!
热处理知识真的很重要,希望楼主多发些这方面的知识。
钢管是怎么热处理的?