Characterizationand Optimization of Pearlite Microstructure Using Persistent Homology andBayesian Optimization

珠光体微观结构的持续同源分析和贝叶斯优化表征与优化

珠光体球化实质上是渗碳体的空间-几何演化过程，本研究采用持续同源性分析方法对珠光体钢渗碳体成分的拓扑特征进行表征，成功区分了层状珠光体微观组织和球状珠光体微观组织。由于珠光体组织钢的力学性能对渗碳体形态构型非常敏感，因此，利用贝叶斯优化方法，提出了一种将持续同源性数字数据反转换为感兴趣的某些特性图像的方法。本文提出的微观结构优化方法为冶金学中持续同源性信息的解释提供了一种方法，并提出了基于数据驱动的持续同源性属性预测和微观结构优化的可行性。

关键词：珠光体组织；持续同源性；微观结构表征；微观结构

1. 引言

共析珠光体具有典型的铁素体和渗碳体交互贯穿层状组织组成的晶体结构，导致珠光体钢具有较高的机械强度。[1]因为微观结构对机械性能具有重大影响，采用球化退火常用于将珠光体钢的片层结构分解为球状结构，以提高塑性、韧性、疲劳寿命和制造成形性。[2~ 5]由于退火过程中显微组织的演变，我们以前的实验证明珠光体球化行为对渗碳体片层的初始形态非常敏感。[6]

传统的基于实验的微观结构表征主要是通过体视学的测量来实现的，这很大程度上依赖于之前的冶金专业知识，往往会导致显著的个体认识上的差别。随着人工智能在材料科学中的应用，基于机器学习的方法越来越多地应用于微观结构鉴别、[7]识别、[8,9]检测[10]等领域，有效地克服了基于实验的表征方法的局限性。然而，大多数这种基于机器学习的微观结构分析缺乏明确的识别微观结构特征的定量策略，因此难以建立数据驱动的微观结构—性质链接。

珠光体球化基本上是渗碳体的空间几何演化过程，这涉及到拓扑数据分析及其推导方法。[11~15]持续同源性是一种很有前途的拓扑分析方法。它可以从复杂的数据空间中捕获潜在的拓扑特征，并同时提供了微观结构的定量定义。[5]我们在之前的研究中提出了一种基于数据驱动的基于持续同源性的方法，该方法考虑了材料的性能预测和微观结构优化，[16,17]可以揭示材料的潜在性能和相应的微观结构。然而，所获得的微观结构与关于持续同源性数字数据跟踪，这仍然不能提供一个明确的冶金特征的定义。因此，为了更好地理解微观结构和性能之间的关系，有必要进一步将持续同源数据转化为微观结构图像。

珠光体球化过程可以借助持续同源性分析的优点，即呈现给定数据空间下的几何演变，因此，本文采用持续同源性分析，进一步表征珠光体组织的拓扑特征。在此基础上，提出了一种基于拓扑信息的数据驱动微观结构优化方法，利用贝叶斯优化方法将数字数据转化为图像。

2. 材料和方法

本研究的材料是以前做研究得到的钢，其化学成分为0.8%的C钢，热轧的钢试样在1 200℃下保温30分钟充分奥氏体化，然后在炉内以1℃/s的冷却速率冷却至室温。随后试样加热到700℃等温退火，时间为0、1和6 个小时，然后以1℃/s冷却速率炉内冷却至室温，形成珠光体组织。机械抛光后的试样用3%体积的硝酸乙醇蚀刻，观察其显微结构。

用扫描电镜(SEM)观察显微组织，将得到的SEM图像进行灰度处理，然后使用ImageJ软件将其转换为二进制模式。阈值由阈值=(平均背景+平均目标)/2确定，其中背景为铁素体相，目标为渗碳体相。

二进制化后的图像随后进行持续同源性分析，以进一步表征微观结构，其中渗碳体作为分析目标。图1说明了持续同源性。待研究的数据空间由一些独立但动画的数据点表示(图1(a))；随着这些动画点的增长，它们会变得彼此相关(图1(b))；此后，一个环关系被称为“诞生”(图1(c))；当环消失时，称为“死亡”(图1(d))。持续化图记录了所有的生命(出生，死亡)(图1(e))。

图1 图示表示持续同源性： (a)和(b)当小珠子直径d小于dbirth数值时，所有小珠子消失；(c)在d = dbirth时，出现环状特征；(d)在d = ddeath时，环特征消失。这种持续同源性由(e)所示的持续图表示

为了获得适合于数据驱动方法的数据模式，使用一个持续图像(PI)[18]对提取的拓扑信息进行矢量化。PI的估计公式如下:

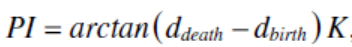    （1）

这里的K为核密度。[19]在这里，将持续图平均分成30 × 30 bins来估计K，即PI作为一个900维的向量计算。

众所周知，在机器学习中，高维数据往往会导致过度拟合。常用的降维技术主要有主成分分析(PCA)、t-分布随机邻居嵌入(t-SNE)和均匀流形逼近与投影(UMAP)。PCA用线性相关变量对高维数据集进行归一化，然后将数据投影到低维空间中，同时保留数据集中的大部分变化。与主成分分析相比，t-SNE是一种尽可能保留原始信息的非线性降维技术。t-SNE在寻找聚类时，通过将相似的观测数据靠近，将不同的观测数据分开来降低维数。UMAP是一种最先进的流形学习和降维算法，创建于2018年，[20]与t-SNE类似，UMAP也是一种非线性降维技术，但具有更高的处理速度和更好的可视化。相比之下，本文采用UMAP进行降维。

采用贝叶斯优化方法进行微观结构优化。高斯过程采用Matern核，[21]初始均值和方差分别设为0和1e-10；选取10个初始点开始优化。采用期望改进(EI)函数作为采集函数，定义为

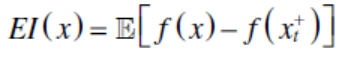    （2）

其中x、x_t⁺、f分别为优化后的参数集、当前最优参数集、一个黑盒函数。一次循环可生成具有最大采集功能输出的潜在微结构图像。

3. 结果与讨论

3.1. 具有持续同源性的微观结构表征

图2(a) -2 (c)分别为未退火、700℃温度下退火1小时和6小时的试样SEM图像(450 × 300像素)。随着退火时间的延长，试样呈现明显的珠光体组织，层状结构逐渐球化。随后，进行持续同源性分析，以进一步表征微观结构。由于足够的数据观察对于执行数据驱动的方法至关重要，因此每个原始的微观结构图像被分割成四个部分，以实现更多的观察。图2(d) -2 (e)显示了二进制模式下的图像块，其中渗碳体成分以黑色标记。

图2 珠光体微观组织： (a)未退火和700℃退火(b) 1小时和(C) 6小时的珠光体显微结构；(d) - (f)分别从(a) - (C)分离出的二进制模式图像。黑色区域表示渗碳体

将分割块(150 × 150像素)作为持续同源性分析的输入，计算渗碳体的拓扑特征，在持续图中记录(d_birth, d_death)地址的输出。图3展示了不同退火时间下的研究图像及其对应的持续图，对比微观结构和持续图，细层状结构(图3(a))和球状结构(图3(c))分别被表征为短寿命和长寿命，这为识别具有持续同源性的珠光体微观结构提供了一种方法。

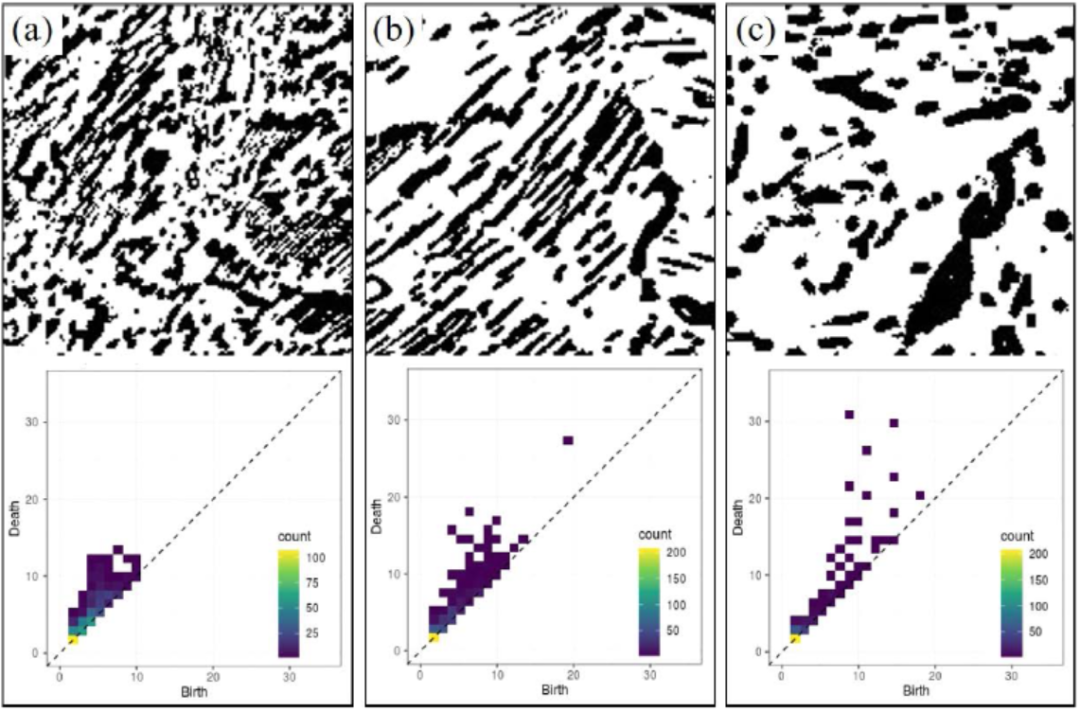
图3  研究映像和他们对应的持续图：(a)不退火和在700℃温度下退火(b) 1小时和(C) 6小时

如前所述，为了获得合适的数据模式，计算PIs以向量化拓扑信息(d_birth、d_death)。采用UMAP算法对所研究的微结构的高维PI数据进行降维和可视化。需要指出的是，学习数据集由3次退火时间下的12个试样观测值组成。由于这些微观结构在之前的实验中已经被很好地区分出来，[6] 因此，所有数据用于训练分类模型，从而进一步识别持久同源性对微观结构表征的有效性。图4是一个二维的UMAP图，显示了UMAP基于持续同源信息成功地分类和识别了不同构型的珠光体微观结构。这一结果为结合持久性同源性和UMAP进行数据驱动的微结构识别开辟了前景。

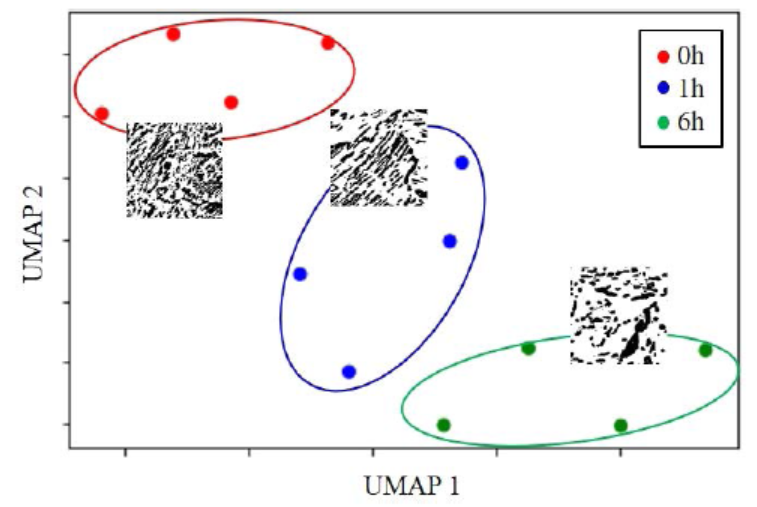
图4  利用UMAP对不同退火时间的珠光体组织进行识别

3.2. 基于贝叶斯优化的微观结构优化

之前提出的基于数据驱动的基于持久性同源性的性能预测和微观结构优化[16,17]可以获得所期望的性能，如高塑性或良好的制造成形性，以及相应的微观组织。然而，实现的显微组织跟踪数字数据关于持久的同源性，这没有提供一个明确的冶金特征的定义。为了更好地理解材料范式，有必要进一步定义基于持续同源性的微观结构。如前所述，珠光体球化有利于珠光体钢的延展性、韧性、疲劳寿命和制造成形性。因此，本研究在现有珠光体微观结构的基础上，利用贝叶斯优化方法，进行了将持续同源数字数据转换为微观结构图像的反向微观结构优化。

图5显示了优化过程，优化从任意创建的初始图像开始。由于珠光体球化产生的是双模层状-球状组织，因此设计了p1、p2、p3、p4、p5五个参数来控制配置，如图6所示。然后，计算初始图像的PI (PI_initial)。这种优化的目的是从数字数据中找到跟踪目标属性的微观结构。因此，通过定义为的Loss函数(PI_initial, PI_target)将PI_initial与目标PI (PI_target)关联起来

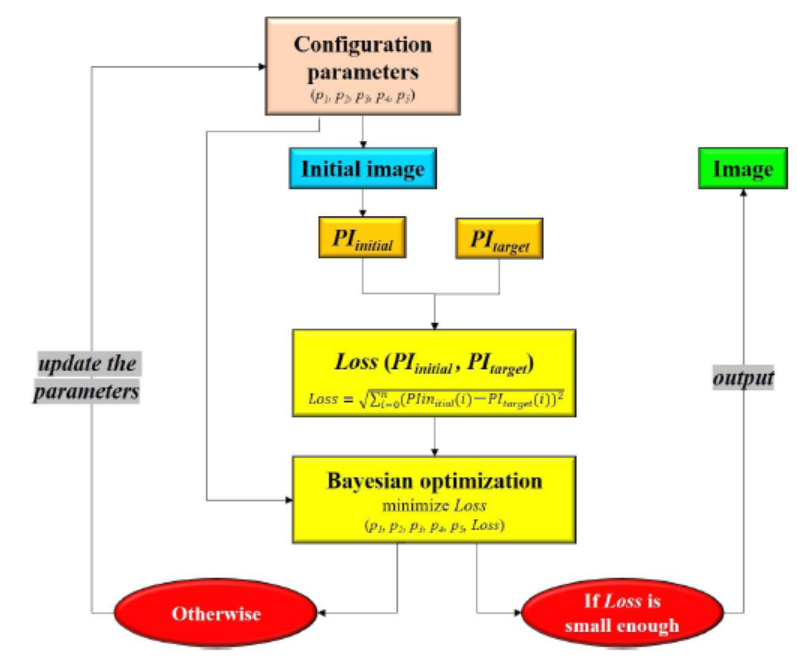
图5  使用贝叶斯优化从持久的同源数据到微观结构图像的逆转换过程。(在线彩色版本。)

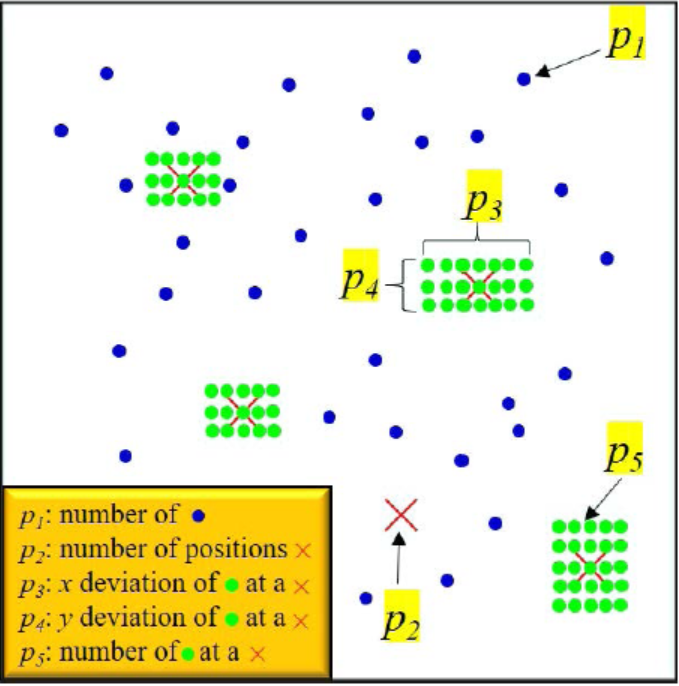
图6  图像构型示意图，其中p1、p2、p3、p4和p5分别表示随机球形粒子数、片层位置数、片层位置粒子的x偏移量、片层位置粒子的y偏移量、片层位置粒子的数量。每个参数的个数表示生成的图像中在随机分布下绘制的像素。 

   （3）

式中，i和n分别表示PI向量的变量个数和变量总数，n由K估计时的bin个数决定，本研究中n为900。因此，将初始图像的配置参数及其Loss生成一个新的向量，表示为(p1, p2, p3, p4, p5, Loss)。然后通过优化p1、p2、p3、p4、p5，将该向量反馈给学习目标为Loss最小化的贝叶斯优化算法。贝叶斯优化后，由优化的p1, p2, p3, p4,和p5绘制图像，当Loss足够小的时候输出，否则，就优化p1, p2, p3, p4,和p5反馈更新配置参数，然后，上述循环执行，直到Loss足够的小。

以提高珠光体钢塑性和成形性能的球状组织为优化目标。为了更好地验证优化后的显微组织，将已知的经过6小时退火的球形组织图像作为目标(图7(a))。图7(b)为初始图像，初始配置参数如图7(d)所示，计算Loss为7.67。图7(c)为循环100次后的输出图像，为球形结构，Loss减小了3.20。通过视觉对比，将初始图像成功地更新为目标图像，表明了该方法的良好潜力。初始图像(图7(b))和输出图像(图7(c))的图像生成方法，首先在初始白背景层(150 × 150像素)上生成图像，然后根据对应的配置参数随机绘制配置，如图6所示。

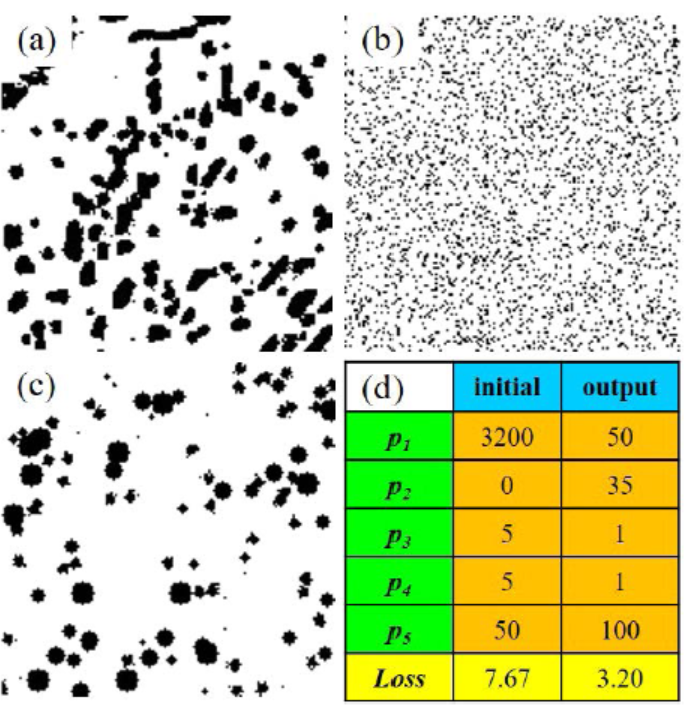
图7  (a)目标图像，(b)初始图像，(c)微观结构优化输出图像。(d)配置参数和初始图像和输出图像的Loss

值得注意的是，由于持续同源性可以表征渗碳体的空间演化，因此本文研究了珠光体微观结构，以说明基于持续同源性的微观结构表征。除显微结构定量外，持续同源性在显微结构分区方面也有很好的应用前景。众所周知，显微结构细分分区常常涉及到对不同灰度级引起的显微图像中纹理的识别，持久性同源性可以通过对每个微观结构组分的生命周期(d_death-d_birth)的智能分水岭的定义来捕捉这种基于纹理的微观结构特征。另一方面，对微观结构优化的配置参数和Loss函数进行了初步设计，智能设计的配置参数和Loss函数可以进一步提高优化性能。本文提出的逆转换方法为冶金学中持续同源性信息的解释奠定了基础，从而完善了之前提出的基于数据驱动的持续同源性属性预测和微观结构优化方法。

此外，众所周知，基于卷积神经网络(CNN)的深度学习类软件在数字图像处理方面表现得非常出色。最近，人们提出了一种用于图像生成的深度卷积生成对抗网络(DCGAN)。[22] DCGAN通过发生器和鉴别器之间的对手来工作，前者扮演艺术家的角色，创造看起来是真实的图像，后者扮演着批评家的角色，以识别所创造的形象的真假。当鉴别器无法识别生成的图像的真假的时候，训练就达到平衡。然而，一些可用的图像数据对于训练良好的图像生成模型是至关重要的，由于微观结构图像是有限的，本研究提出了一种简化的独立设计方法。设计了5个参数来控制作为发生器的图像的配置，并通过贝叶斯优化来识别作为鉴别器的生成图像的配置。然而，仅仅五个配置参数确实不足以生成所需的数字图像，因此，DCGAN将用于进一步执行图像生成任务，以服务于之前提出的数据驱动的属性预测和微观结构优化方法。

4. 总结

珠光体组织的表征采用持续同源性分析来表征，持续同源性分析表明，层状渗碳体和球状渗碳体分别具有短寿命和长寿命的特征，为珠光体显微组织的识别提供了一种新的方法。根据规约，珠光体微观结构的不同配置进一步分类和识别使用UMAP。基于持续同源信息，利用贝叶斯优化算法将数字数据逆转换为图像，对目标图像进行微观结构优化，逆转换提供了具有冶金解释途径的持续同源性信息。

贡献

作者的贡献是均等的：Kazuki Kiyomura进行了这项研究；Zh-Lei Wang撰写稿件；Toshio Ogawa和Yoshitaka Adachi指导监督了这项研究。

参考文献

1) E. M. Taleff, J. J. Lewandowski and B. Pourladian: JOM, 54 (2002),25. https://doi.org/10.1007/BF02700982

2) H. Rastegari, A. Kermanpur, A. Najafizadeh, D. Porter and M. Somani: J.Alloy. Compd., 626 (2015), 136. https://doi.org/10.1016/j. jallcom.2014.11.170

3) H. Hwang and B. C. De Cooman: Steel Res. Int., 87 (2016),112. https://doi.org/10.1002/srin.201400591

4) K. H. Kim, S. D. Park, J. H. Kim and C. M. Bae: Met. Mater. Int.,18 (2012), 917. https://doi.org/10.1007/s12540-012-7002-3

5) Z. Lü, H. Zhang, Q. Meng, Z. Wang and W. Fu: J. Iron Steel Res. Int.,23 (2016), 145. https://doi.org/10.1016/S1006-706X(16)30026-7

6) Y. T. Wang, Y. Adachi, K. Nakajima and Y. Sugimoto: Acta Mater.,58 (2010), 4849. https://doi.org/10.1016/j.actamat.2010.05.023

7) J. Gola, J. Webel, D. Britz, A. Guitar, T. Staudt, M. Winter and F.Mücklich: Comput. Mater. Sci., 160 (2019), 186.https://doi.org/10.1016/j.commatsci.2019.01.006

8) D. L. Naik, H. U. Sajid and R. Kiran: Metals, 9 (2019),546. https://doi.org/10.3390/met9050546

9) K. Tsutsui, H. Terasaki, K. Uto, T. Maemura, S. Hiramatsu, K. Hayashi,K. Moriguchi and S. Morito: Mater. Today Commun., 25 (2020),101514. https://doi.org/10.1016/j.mtcomm.2020.101514

10) M. Müller, G. Stanke, U. Sonntag, D. Britz and F. Mücklich: Metallogr.Microstruct. Anal., 9 (2020), 709. https://doi.org/10.1007/ s13632-020-00676-9

11) G. Carlsson: Bull. Am. Math. Soc., 46 (2009), 255. https://doi.org/10.1090/S0273-0979-09-01249-X

12) H. Edelsbrunner, D. Letscher and A. Zomorodian: Proc. 41st AnnualSymp. on Foundations of Computer Science, IEEE, Piscataway, NJ, (2000), 454.https://doi.org/10.1109/SFCS.2000.892133

13) A. Zomorodian and G. Carlsson: Discrete Comput. Geom., 33 (2005),249. https://doi.org/10.1007/s00454-004-1146-y

14) A. Hirata, L. J. Kang, T. Fujita, B. Klumov, K. Matsue, M. Kotani, A.R. Yavari and M. W. Chen: Science, 341 (2013), 376. https://doi. org/10.1126/science.1232450

15) H. Edelsbrunner and J. Harer: Computational Topology: an Introduction,American Mathematical Society, Providence, (2010), 178.

16) Z. L. Wang, T. Ogawa and Y. Adachi: Adv. Theory Simul., 3 (2020),1900227. https://doi.org/10.1002/adts.201900227

17) Z. L. Wang, T. Ogawa and Y. Adachi: Adv. Theory Simul., 3 (2020),2000040. https://doi.org/10.1002/adts.202000040

18) H. Adams, T. Emerson, M. Kirby, R. Neville, C. Peterson, P. Shipman,S. Chepushtanova, E. Hanson, F. Motta and L. Ziegelmeier: J. Mach. Learn.Res., 18 (2017), 1. https://jmlr.org/papers/v18/16-337.html

19) S. J. Sheather and M. C. Jones: J. R. Stat. Soc. Ser. B, 53 (1991),683. https://doi.org/10.1111/j.2517-6161.1991.tb01857.x

20) L. McInnes, J. Healy and J. Melville: arXiv:1802.03426, (2018),https://arxiv.org/pdf/1802.03426.pdf?kl=viewed, (accessed 2018-09-02).

21) M. G. Genton: J. Mach. Learn. Res., 2 (2001), 299. https://dl.acm.org/doi/abs/10.5555/944790.944815

22) A. Radford, L. Metz and S. Chintala: arXiv preprint arXiv:1511.06434,(2015), https://arxiv.org/pdf/1511.06434.pdf%C3, (accessed 2016-01-07).

作者

Kazuki KIYOMURA：Department of MaterialsScience and Engineering, Nagoya University, Furo-cho, Chikusa-ku, Nagoya,464-8601 Japan.

Zhi-Lei WANG*：Department of MaterialsScience and Engineering, Nagoya University, Furo-cho, Chikusa-ku, Nagoya,464-8601 Japan. 通讯作者E-mail: wang.zhilei@material.nagoya-u.ac.jp

Toshio OGAWA：Department of MaterialsScience and Engineering, Nagoya University, Furo-cho, Chikusa-ku, Nagoya,464-8601 Japan.

Yoshitaka ADACHI：Department of Materials Science and Engineering,Nagoya University, Furo-cho, Chikusa-ku, Nagoya, 464-8601 Japan.

唐杰民2022年三月上旬在黄山翻译自日本<ISIJ International>2022年2月期刊，水平有限，其实没有真正理解吃透这种方法，仅仅是从字面上来翻译，请各位看官给与指正。

这期杂志都是这方面的内容，上周已经发送了一篇，还有两篇这方面文章。来源：常州精密钢管博客网。