详述弹性力学问题的求解方法,看完让你茅塞顿开!
弹性力学空间问题的基本方程有15个方程,分别为3个平衡方程,6个几何方程和6个物理方程,未知数也是15个,分别为3个位移分量,6个应力分量和6个应变分量。只要求出这15个未知量,就可以解决工程中的强度(依据应力、应变)、刚度(依据应变、位移)和稳定性(临界载荷可由应力给出)。然而,问题在于平衡方程和几何方程为微分方程,这给求解带来了极大的挑战性。
平衡方程:
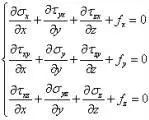
几何方程:
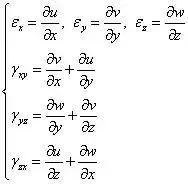
物理方程:
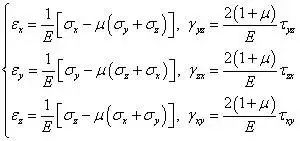
在力学分析中有一类非常有效的“以退为进” 分析方法,在面对一个非常棘手的问题时,先通过一定的假设将问题简化,先求解简化问题,然后再逐步增加问题的难度,最终达到解决问题的目的。假设有一维弹性力学问题,除σx、εx、u、fx不为0以外,其它量均为0,此时弹性力学基本方程简化为:
平衡方程:
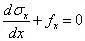
几何方程:
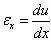
物理方程:
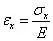
先积分平衡方程,得σx=-fxx+C1,将其代入物理方程,得εx=(-fxx+C1)/E,再将应变代入几何方程,得u=(-fxx²)/2E+(C1x)/E+C2。其中C1、C2为积分常数,需要通过边界条件来确定。
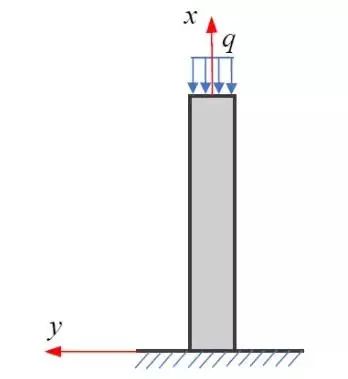
图1 一维弹性力学问题:立柱
设有高为h的立柱,如图1所示,密度为ρ, 则体力fx=-ρg,下端为固定端,上端受均布载荷q作用。此时写边界条件,如下:
上端x=h处:
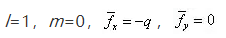
代入应力边界条件,有
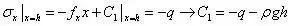
在固定端上写位移边界条件,由于位移分量除u 以外,均为0,在边界上有
下端x=0处:
u=0(v=0和əv/əx=0自然满足)
代入位移边界条件,有
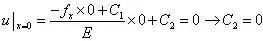
因此,将常数C1、C2带回解中,得
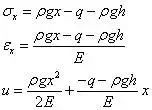
求解完毕。
在数学中,求解方程组通常可采用消元法,先得到只有一个未知数的方程并求解,然后逐一代回原方程组得到其它未知数。对于一般弹性力学问题,也可以采用消元法,只不过弹性力学方程组很难消元至只含有一个未知量的方程,但消元的思想仍然可以借鉴。
我们把弹性力学未知量分为应力分量、应变分量和位移分量三类,如果将应力和应变都用位移表示,使得方程中只含有位移未知量,达到消元的目的并求解,这种方法称之为位移法;当所有的未知量均由应力分量表示,使得方程中只含有应力未知量,达到消元的目的并求解时,称为应力法。所谓的位移法和应力的关键在于选择位移,还是应力作为未知量。还有些题目,如温度应力,将问题分解为两步求解:第一步不考虑实际边界,只考虑温度引起的变形,采用位移法;第二步,叠加应力,以满足真实的边界条件,采用应力法。这种问题混合使用了位移法和应力法,被称为混合法。
平面问题(包括平面应力问题和平面应变问题)求解在弹性力学中占有重要地位,以下我们以平面应力问题为例,说明二维平面问题的求解。对于平面应力问题,有
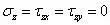
弹性力学基本方程简化为
平衡方程:
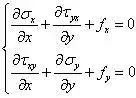
几何方程:
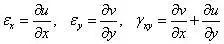
物理方程:
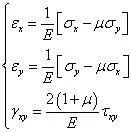
下面分别讨论利用位移法和应力法求解上述平面应力问题的方程组。对于平面应变问题,只需要将弹性常数E变换为外E/1-μ²,将μ转换为μ/1-μ。
位移法:
位移法的目标是将所有的未知量由位移分量表示,观察方程组发现:几何方程中,应变分量已经由位移分量给出,而物理方程描述的是应变与应力之间的关系,先将物理方程变形为用应变表示应力的形式,有
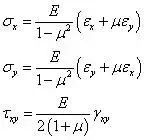
将几何方程代入上式有
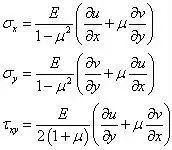
现在应力分量也由位移分量表出,将上式代入平衡方程,得
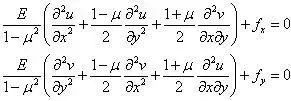
上式为用位移表示的平衡方程。现在可以看出, 上式中含有u 和v 两个未知量,共两个方程, 理论上可以求解。但是很多力学家验证,直接求解上述方程组的难度很大,多数情况下需要采用有限差分、有限元等数值方法进行求解。
这里,我们仍然以图1所示的一维问题为例, 来说明位移法的求解过程。对于一维问题,上式中,v=fy=ə/əy=0,一维问题不考虑横向效应,μ=0,因此用位移表示的平衡方程简化为
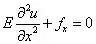
对上式积分两次,得
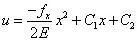
其中,fx=-ρg,C1和C2为积分常数,需要通过边界条件确定。从题设可知,x=0处为位移边界条件u=0,将上式代入,得C2=0。
在x=h处为应力边界条件。应力边界条件公式为
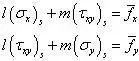
将下式代入上式表示的边界条件
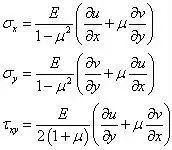
得
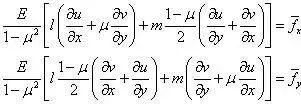
这里可以看出,应力边界条件实际上可以转化为位移边界条件。具体到本问题,考虑v=fy=ə/əy=0,且l=1,m=0。上式变为

依据
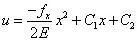
得əu/əx=(ρg/E)x+C1,将其代入边界条件式

得
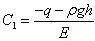
将C1和C2代回式
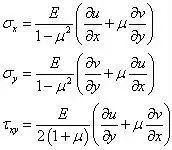
得
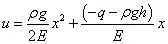
获得位移分量后,通过几何方程,得到应变分量εx=(ρgx-q-ρgh)/E,再利用物理方程得到应力分量σx=ρgx-q-ρgh,与下式表示的解完全一致。
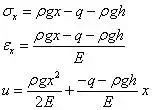
应力法:
下面我们来考虑如何利用应力法求解二维弹性力学问题,目标为将所有未知量都用应力表示,即所有方程中,不再出现应变分量和位移分量。依然考虑平面应力状态下的基本方程,如下所示:
平衡方程:
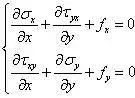
几何方程:
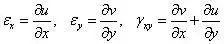
物理方程:
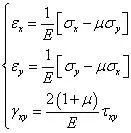
其中,平衡方程中只含有应力分量,无需过多关注。下面重点来看几何方程和物理方程。首先看几何方程,从方程形式看,2个位移分量决定了3个应变分量,那么3个应变分量之间很可能不完全独立,那么它们应该满足什么关系呢?为了说明3个分量之间的关系,我们进行如下推导:

请关注最后导出来的式(13),这个式子把三个应变分量写在同一个方程中,明确无误的表明了3个应变分量并非完全独立,它们就像一条绳上的3个蚂蚱,只要有一个变动,另外的两个也可能跟着发生变动。3个应变分量满足的这一关系称为变形协调方程(或相容方程),这一关系最早由圣维南于1864年导出,1866 年,贝尔特拉米(Eugenio Beltrami, 1835-1900.意大利著名数学家)对其进行了严格证明。变形协调方程说明了真实弹性体发生变形时需要满足的条件,即某一点的应变分量满足上式时才是真实的,如果不满足上式, 对于真实的弹性体,很可能发生了断裂、质点堆叠等不可预估的情形,超出了弹性力学的研究范畴。
再回到平面问题基本方程,如果将物理方程代入变形协调方程,就可以得到用应力表示的变形协调方程,有
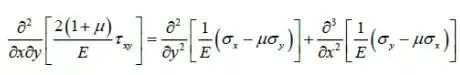
现在已经看到,几何方程和物理方程已经转化为上式,完全由应力分量给出,与平衡方程
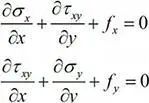
一起组成方程组,3个方程(2个平衡方程+1变形协调方程)求解3个未知量(σx、σy、τxy),为封闭方程组。继续沿着消元的思想,利用平衡方程,还可以将变形协调方程中的τxy消去, 我们进行如下推导:

上式为考虑了平衡方程的相容方程,只要找到上式的解,就可以利用平衡方程,求出τxy,再依据物理方程,求出应变分量,最后依据几何方程,求出位移分量。
如果仍考虑图1所示的一维问题,仍有v=fy=ə/əy=0,以及μ=0,上式将简化为
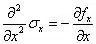
由于,fx=-ρg为常数,为ə²/əx²,积分后有
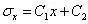
代入物理方程,得
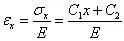
再代入几何方程,有
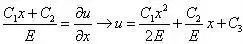
考虑固定端位移边界条件,有
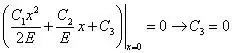
还有两个未知数C1和C2,但是顶部应力边界条件只能写出一个方程,需要再补充一个应力边界条件。为此,考虑固定端,去掉约束后, 下端约束反力为ρgh+q,如
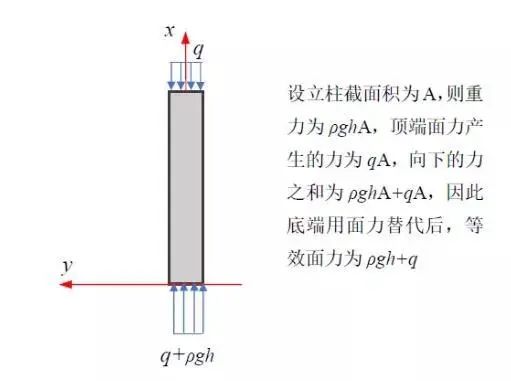
图2 固定端等效面
以下为应力边界条件:
上端:
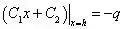
下端:
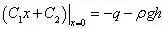
联列两个应力边界条件,得
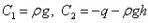
代入应力、应变、位移表达式,得

利用应力法求解也与前面的解一致。
平面问题的求解在弹性力学中占有非常重要的地位,是弹性力学的重点内容。本文虽然推导了二维平面问题应力法和位移法的基本方程,但所举例子均为一维问题,没有真正涉及二维问题的求解,目的在于理解力法和位移法的求解过程。实际上,二维问题的求解难度要远远大于一维问题,时至今日,利用位移解析法求解二维问题的例子仍然很少。
来源:常州精密钢管博客网:力学酒吧,作者:张伟伟
- 随机文章
- 热门文章
- 热评文章






 欢迎你第一次访问网站!
欢迎你第一次访问网站!
这外材料的锅炉管你们仁成钢管厂好不好做?
钢材的知识真的很博大精深,学习中......